Edit: Ich kapier’s nicht
Dreiecke rastern
- Krishty
- Establishment
- Beiträge: 8405
- Registriert: 26.02.2009, 11:18
- Benutzertext: state is the enemy
- Kontaktdaten:
Dreiecke rastern
Bei komplett bedeckten Pixeln wird nur die Diagonale abgelaufen, weiß sind sie aber trotzdem?
Edit: Ich kapier’s nicht

Edit: Ich kapier’s nicht
Re: Showroom - Aktuelle Arbeiten und Projekte
Blöde Frage: Wäre es evtl. einfacher das ganze in C# zu schreiben, nur schon damit du debuggen kannst? Die Shader-Operationen könnte man ja nachbauen. Ich habe mich schon selbst für kleinere Aufgaben über die fehlenden Debug-Möglichkeiten in Shadern geärgert und mir sowas überlegt. Jedenfalls wünsche ich viel Erfolg.
Blood of the Undead https://falkenbrew.itch.io/blood-of-the-undead
- starcow
- Establishment
- Beiträge: 590
- Registriert: 23.04.2003, 17:42
- Echter Name: Mischa Schaub
- Wohnort: Zürich
- Kontaktdaten:
Re: Showroom - Aktuelle Arbeiten und Projekte
Wie wichtig sind den die Fälle, bei welchen ein Pixel von mehr als einer Dreieckslinie geschnitten wird? Fällt das denn optisch überhaupt ins Gewicht?
Weil bei Berücksichtigung von nur einer Linie, wärs wohl sehr viel einfacher...
Weil bei Berücksichtigung von nur einer Linie, wärs wohl sehr viel einfacher...
- Schrompf
- Moderator
- Beiträge: 5330
- Registriert: 25.02.2009, 23:44
- Benutzertext: Lernt nur selten dazu
- Echter Name: Thomas
- Wohnort: Dresden
- Kontaktdaten:
Re: Showroom - Aktuelle Arbeiten und Projekte
Ich hab hier mal ne Zeichnung gemacht:
Normalerweise geht der Algorithmus von Schnittpunkt zu Schnittpunkt im Uhrzeigersinn und berechnet für jedes Teilstück den (vorzeichenbehafteten) Flächeninhalt. Von ABEintritt zu ABAustritt geht es rechts hoch, das Rechteck ab Höhe ABEintritt bis Bodenhöhe ist positiv, die Schräge nach rechts oben ist 0.5 * Breite * Höhe, nach rechts ist +X, nach oben +Y. Weiter zum Teilsegment ABAustritt -> BCEintritt. Gerade nach rechts, positiver Beitrag. Nächstes Teilsegment BCEintritt zu BC-Austritt: das Rechteck BC-Eintritt bis Boden geht über die komplette Höhe, aber die Schräge ist 0.5 * Breite * Höhe, und Ydiff ist in diesem Fall negativ, zieht also die Schräge in diesem Fall ab. BC-Austritt bis CA-Eintritt ist gerade nach unten, hat also Xdiff von 0 und macht gar nix. Und dann kommt CA-Eintritt -> CA-Austritt: das Rechteck von Höhe CA-Eintritt bis zum Boden ist negativ, weil Xdiff negativ ist, der Teil über dem Boden wird also vom Gesamt-Flächeninhalt abgezogen. Zusätzlich kommt die Schräge dazu, die wegen Xdiff negativ und Ydiff positiv auch negativ eingeht, also noch mehr vom Flächeninhalt abzieht.
Auf die Art ergänzen sich alle Anteile zum exakten Gesamt-Flächeninhalt, solange das Dreieck im Uhrzeigersinn orientiert ist. Als ich das raus hatte und damit alle Fallunterscheidungen und Sortierungen loswerden konnte, die ich vorher erst mühsam eingebaut hatte, war ich ein sehr glücklicher Schrompf. Nur dass es im Gesamtsystem grausam versagte. Warum?
Schauen wir uns mal dieses Beispiel an. Ich habe es bewusst gewählt, um genau den Fall nachzustellen, der Dir (und vorher mir) Verwirrung stiftet.
Man sieht hier: dadurch, dass die drei Kanten alle außerhalb passieren, quetschen sich Eintrittspunkt und Austrittspunkt jeweils in die Ecke, die der Kante am nächsten sind. ABRein zu ABRaus ist ein Null-Beitrag, ABRaus zu BCRein ist die eigentliche Füllung, BCRein zu BCRaus ist Null, BCRaus zu CARein ist 0 breit, CARein zu CARaus ist Null.
Der kritische Teil ist das letzte Teilsegment auf der Uhrzeigerrunde: CARaus zu ABRein. Und nach wirklich langem harten Nachdenken und einer Stuhlgangspause kam mir hier die Erkenntnis: die Schrägen dieser Segmente sind gar nicht echt. Die Rein-Zu-Raus-Kanten sind echte Kanten des Dreiecks, deren Schrägen müssen wir korrekt einberechnen. Aber die Zwischen-Segment vom Raus der einen Kante zum Rein der anderen Kante sind nicht echt. Die bedeuten nur, dass der Vertex, der im Uhrzeigersinn zwischen den beiden liegt, weit außerhalb ist. Wir dürfen für die drei Zwischen-Kanten-Segmenten also nicht einfach die Schräge berechnen. Stattdessen biegen wir die Schräge nach außen. In welche Richtung genau wir biegen, ist eigentlich nicht wichtig. Der wichtige Beitrag ist eigentlich nur, dass der Schräganteil des Flächeninhalts sich von "0.5 * Breite * Höhe" zu entweder 0x oder 1x verschiebt. Und das macht im Shadersource die Variable cornerClipSegCorrection.
Hier im Beispielfall geht CARaus zu ACRein die Diagonale, die Schräge würde also den halben Flächeninhalt wieder abziehen. Aber wenn man sich die Schräge in Richtung des Punktes C umgebogen vorstellt, reduziert sich der Schräganteil auf 0x und es wird nichts mehr abgezogen.
Die Visualisierung für den einen Testpixel zeigt aber weiterhin die Schräge, weil es mir zuviel Mühe war, auch die Visualisierung zu korrigieren, nachdem ich das Problem verstanden und behoben hatte.
@marcgfx: ich hatte schon erwogen, das in C++ nachzubauen, um es debuggen zu können. Aber man hat im Shader halt andere Möglichkeiten der Fehlersuche, man muss sie nur nutzen.
@starcow: Hier isses nicht so wichtig, außer vielleicht an den Spitzen. Aber ich rechne spätestens bei den Sekundäranwendungen des Volume Ray Castings mit Dreiecken von nur eins zwei Pixeln Größe. Und dann muss es exakt sein.
Früher mal Dreamworlds. Früher mal Open Asset Import Library. Heutzutage nur noch so rumwursteln.
- starcow
- Establishment
- Beiträge: 590
- Registriert: 23.04.2003, 17:42
- Echter Name: Mischa Schaub
- Wohnort: Zürich
- Kontaktdaten:
Re: Showroom - Aktuelle Arbeiten und Projekte
Sehr spannend! Danke für die Einblicke Schrompf!
Ich hätte dir allenfalls auch noch einen alternativen (präzisen) Lösungsansatz. Den habe ich jetzt zwar noch nicht ganz konkret ausformuliert, da ich mir nicht sicher war, wie zufrieden du bereits mit deiner Lösung bist - ich will ihn dir aber trotzdem nicht vorenthalten. Ich glaube, er wird weitesgehend ohne Sonderfälle auskommen.
Der Ansatz basiert darauf, dass die durch das Dreieck bedeckte Pixelfläche immer konvex sein muss - ein konvexes Polygon.
Man muss also nur die Eckpunkte dieses Polygons bestimmen, dieses dann triangulieren (in meiner Grafik die blauen Dreieicke) und anschliessend die Fläche der einzelnen Dreiecke zusammenzählen.
Ich lehne mich mal aus dem Fenster und sage, dass das finden der Eckpunkte (in meiner Grafik die orangen Punkte) keine grosse Sache sein sollte.
Man muss berücksichtigen, dass ein oranger Punkt nicht nur ein Schnittpunkt zweier Geraden sein kann, sondern auch ein Eckpunkt des Dreiecks oder ein Eckpunkt des Pixel-Quadrates.
Hat man diese Punkte, kann eigentlich nicht mehr viel schief gehen.
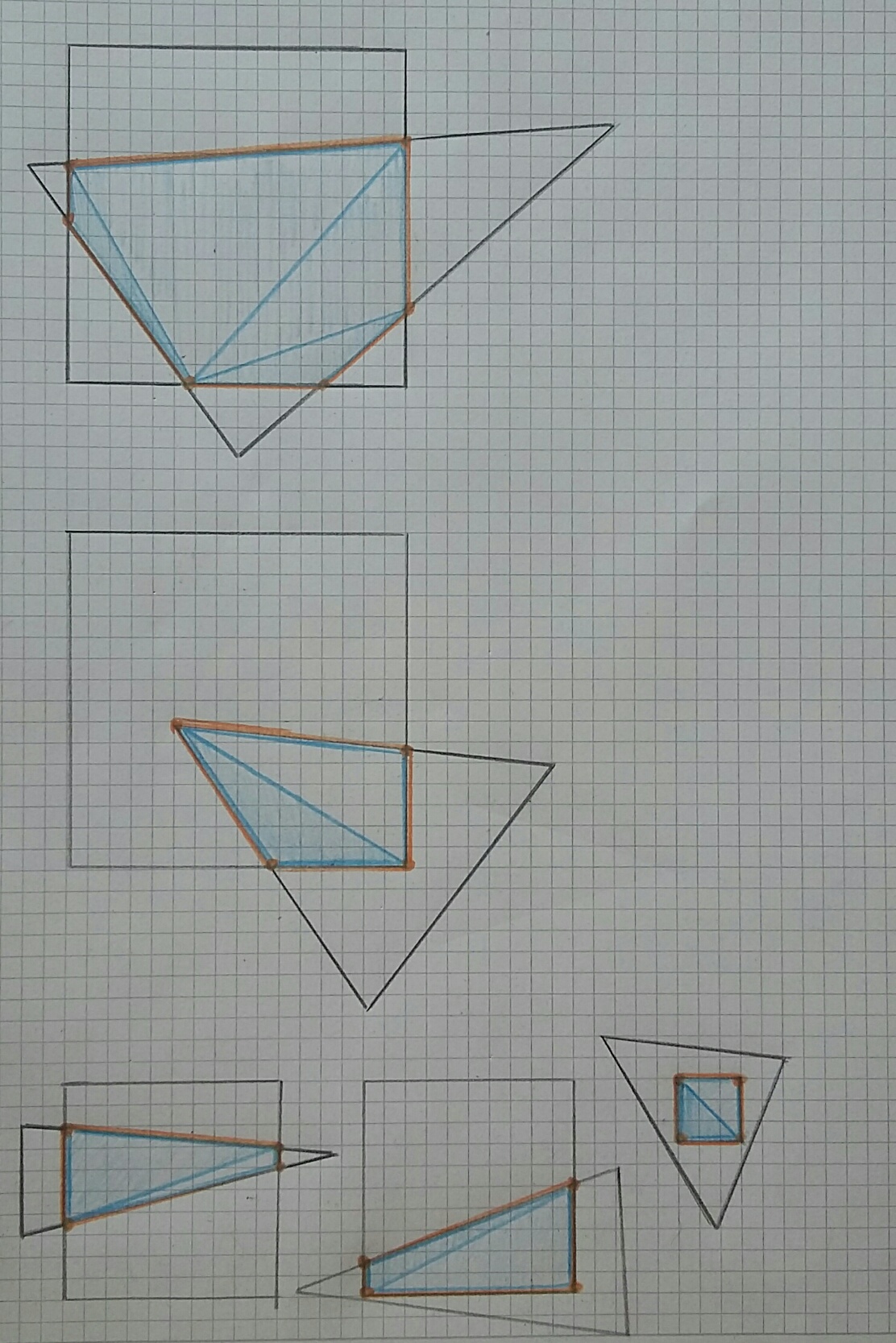
Es gelten zwei simple Regeln:
- Lieg ein Eckpunkt des Pixel-Quadrates innerhalb des Dreicks, so ist dieser Eckpunkt ein oranger Punkt.
- Liegt ein Eckpunkt des Dreieck innerhalb des Pixel-Quadrates, so ist dieser Eckpunkt ein oranger Punkt.
Falls der Ansatz dein Interesse finden sollte, kann ich auch nochmals versuchen, das ganze zu konkretisieren.
Ich hätte dir allenfalls auch noch einen alternativen (präzisen) Lösungsansatz. Den habe ich jetzt zwar noch nicht ganz konkret ausformuliert, da ich mir nicht sicher war, wie zufrieden du bereits mit deiner Lösung bist - ich will ihn dir aber trotzdem nicht vorenthalten. Ich glaube, er wird weitesgehend ohne Sonderfälle auskommen.
Der Ansatz basiert darauf, dass die durch das Dreieck bedeckte Pixelfläche immer konvex sein muss - ein konvexes Polygon.
Man muss also nur die Eckpunkte dieses Polygons bestimmen, dieses dann triangulieren (in meiner Grafik die blauen Dreieicke) und anschliessend die Fläche der einzelnen Dreiecke zusammenzählen.
Ich lehne mich mal aus dem Fenster und sage, dass das finden der Eckpunkte (in meiner Grafik die orangen Punkte) keine grosse Sache sein sollte.
Man muss berücksichtigen, dass ein oranger Punkt nicht nur ein Schnittpunkt zweier Geraden sein kann, sondern auch ein Eckpunkt des Dreiecks oder ein Eckpunkt des Pixel-Quadrates.
Hat man diese Punkte, kann eigentlich nicht mehr viel schief gehen.
Es gelten zwei simple Regeln:
- Lieg ein Eckpunkt des Pixel-Quadrates innerhalb des Dreicks, so ist dieser Eckpunkt ein oranger Punkt.
- Liegt ein Eckpunkt des Dreieck innerhalb des Pixel-Quadrates, so ist dieser Eckpunkt ein oranger Punkt.
Falls der Ansatz dein Interesse finden sollte, kann ich auch nochmals versuchen, das ganze zu konkretisieren.
- Schrompf
- Moderator
- Beiträge: 5330
- Registriert: 25.02.2009, 23:44
- Benutzertext: Lernt nur selten dazu
- Echter Name: Thomas
- Wohnort: Dresden
- Kontaktdaten:
Re: Showroom - Aktuelle Arbeiten und Projekte
Die Idee gefällt mir. Das Ding ist ja garantiert immer konvex. Das heißt, Du kannst einen Fächer rundherum aufspannen, kennst genau die Abfolge der Punkte und berechnest mit dem Kreuzprodukt den Flächeninhalt aller vier entstehenden Dreiecke. Wenn irgendwelche Punkte zusammenfallen, kommt für die 0 raus. Reihenfolge ist wie bei meiner Lösung im Uhrzeigersinn. Schön. Kann sein, dass es gar nicht schneller ist als meine Lösung, weil Du vier Wurzeln ziehen musst, aber es ist einen Versuch wert. Und der Code ist sicher verständlicher als meiner.
Naja... ne. Die Lösung leidet genauso wie meine unter dem Problem der Falschen Diagonalen. Und hier müsstest Du aufwändig die Eckpunkte in die Abfolge der Ein- und Austrittspunkte einsortieren. Vielleicht kann man auch einfach die Flächeninhalte aufsummieren und würde durch das Winding und die daraus entstehenden Vorzeichen beim richtigen Wert rauskommen... ich weiß nicht.
Wenn Du Zeit und Lust hast, kopier Dir mal den Shadertoy-Code von oben und probier Dein Glück. Ich werde meine Aufmerksamkeit jetzt erstmal auf die sich daraus ergebenden Möglichkeiten richten.
Naja... ne. Die Lösung leidet genauso wie meine unter dem Problem der Falschen Diagonalen. Und hier müsstest Du aufwändig die Eckpunkte in die Abfolge der Ein- und Austrittspunkte einsortieren. Vielleicht kann man auch einfach die Flächeninhalte aufsummieren und würde durch das Winding und die daraus entstehenden Vorzeichen beim richtigen Wert rauskommen... ich weiß nicht.
Wenn Du Zeit und Lust hast, kopier Dir mal den Shadertoy-Code von oben und probier Dein Glück. Ich werde meine Aufmerksamkeit jetzt erstmal auf die sich daraus ergebenden Möglichkeiten richten.
Früher mal Dreamworlds. Früher mal Open Asset Import Library. Heutzutage nur noch so rumwursteln.
- starcow
- Establishment
- Beiträge: 590
- Registriert: 23.04.2003, 17:42
- Echter Name: Mischa Schaub
- Wohnort: Zürich
- Kontaktdaten:
Re: Showroom - Aktuelle Arbeiten und Projekte
Du hast leider recht. Die Reihenfolge der Punkte ist relevant und wird zum Problem. Ich sehe dabei auch nur die Möglichkeit, die Punkte in einem zweiten Schritt zu sortieren. Ob dies dann aber so, in der Form, mit deiner Variante noch mithalten können wird, bezweifle ich leider.
- Schrompf
- Moderator
- Beiträge: 5330
- Registriert: 25.02.2009, 23:44
- Benutzertext: Lernt nur selten dazu
- Echter Name: Thomas
- Wohnort: Dresden
- Kontaktdaten:
Re: Dreiecke rastern
Ne, das passt, und ich werde es die nächsten Tage mal ausprobieren: es reicht, zwischen dem Austrittspunkt der einen Kante und dem Eintrittspunkt der nächsten Kante einfach den dortigen Punkt mitzurechnen. Ich mach mal fix ne Zeichnung.
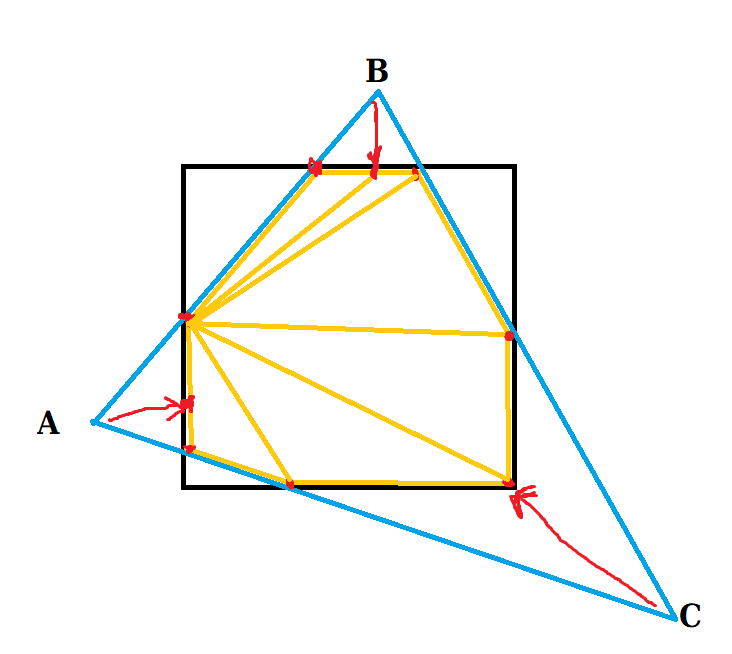
Damit meine ich: wir fächern Dreiecke auf, aber nicht nur zu jedem Schnittpunkt, sondern zusätzlich auch zu jedem Vertex zwischen den Kanten. Die Vertizes werden genauso wie die Schnittpunkte in den Pixelbereich reingezerrt und landen damit entweder auf der Außenkante zwischen den Schnittpunkten (im Bild obere Kante) oder in der Ecke (im Bild rechts unten). Und damit funktioniert das ganze transparent und ohne Fallunterscheidung. Damit werden halt aus 6 Schnittpunkten (== 4 Dreiecke) dann 9 Schnittpunkte (== 7 Dreiecke), aber es kann sein, dass das immer noch performt.
Damit meine ich: wir fächern Dreiecke auf, aber nicht nur zu jedem Schnittpunkt, sondern zusätzlich auch zu jedem Vertex zwischen den Kanten. Die Vertizes werden genauso wie die Schnittpunkte in den Pixelbereich reingezerrt und landen damit entweder auf der Außenkante zwischen den Schnittpunkten (im Bild obere Kante) oder in der Ecke (im Bild rechts unten). Und damit funktioniert das ganze transparent und ohne Fallunterscheidung. Damit werden halt aus 6 Schnittpunkten (== 4 Dreiecke) dann 9 Schnittpunkte (== 7 Dreiecke), aber es kann sein, dass das immer noch performt.
Früher mal Dreamworlds. Früher mal Open Asset Import Library. Heutzutage nur noch so rumwursteln.
Re: Dreiecke rastern
Per SDF rastern könnte einfacher/schneller sein, wenn auch mathematisch ungenauer (Der Fehler: Man hat runde Pixel statt quadratische, und aus "Abstand" lässt sich nicht überall exakt auf "Kreisbedeckung" schließen, an den Ecken z.B.).

Ich glaube es gibt sogar ein Malprogramm welches per SDF rastert, habe leider den Namen vergessen.
Vielleicht hast du auch ein Einsatzgebiet im Hinterkopf wo du das exakte Ergebnis benötigst, dann habe ich nichts gesagt ;) Aber falls es nur um Optik geht, lohnt es ja manchmal, mit einer Näherung zu leben. Im Prinzip hatte ich bei meinem letzten AO-Experiment ja dasselbe gemacht: Ein aufwändigeres Integral durch eine ungenauere SDF-Abschätzung ersetzt.
SDF-Funktionen hätten noch den Vorteil, dass es Linien mit Line-Thickness, Punkte, Quads u.a. gibt, ohne das aus Dreiecken aufbauen zu müssen.
Ich glaube es gibt sogar ein Malprogramm welches per SDF rastert, habe leider den Namen vergessen.
Vielleicht hast du auch ein Einsatzgebiet im Hinterkopf wo du das exakte Ergebnis benötigst, dann habe ich nichts gesagt ;) Aber falls es nur um Optik geht, lohnt es ja manchmal, mit einer Näherung zu leben. Im Prinzip hatte ich bei meinem letzten AO-Experiment ja dasselbe gemacht: Ein aufwändigeres Integral durch eine ungenauere SDF-Abschätzung ersetzt.
SDF-Funktionen hätten noch den Vorteil, dass es Linien mit Line-Thickness, Punkte, Quads u.a. gibt, ohne das aus Dreiecken aufbauen zu müssen.
- Schrompf
- Moderator
- Beiträge: 5330
- Registriert: 25.02.2009, 23:44
- Benutzertext: Lernt nur selten dazu
- Echter Name: Thomas
- Wohnort: Dresden
- Kontaktdaten:
Re: Dreiecke rastern
SDF ist auch ne coole Idee, aber ich glaube, das rockt nur für Dreiecke sehr viel größer als ein Pixel. Sieht man hübsch an dem Minidreieck im Beispielbild, linke untere Ecke: der Pixel ist ~halb gefüllt, weil die Mitte des Messbereichs fast genau auf der unteren Dreieckskante liegt. Wenn das Dreieck oberhalb dieser Kante weitergehen würde, wär "die Hälfte" auch das korrekte Ergebnis. Aber das Dreieck ist an der Stelle schon sehr schmal, und die SDF kann sowas natürlich nicht abbilden.
Ich habe inzwischen ne andere Idee gehabt, die für alle konvexen Messbereiche funktioniert: man rechnet den Flächeninhalt des zurechtgestutzten Dreiecks aus, wie als wäre nix. Und dann rechnet man für die Zwischen-Den-Kanten-Geraden die Außenflächen dazu. Die Strecken zwischen Kante-Eintritt-In-Messbereich und Kante-Austritt-Aus-Messbereich sind ja "echte" Kanten, die nehmen wir als echte Schrägen. Die Strecken zwischen Austritt-Vorkante-Aus-Messbereich und Eintritt-Nachfolgekante-In-Messbereich sind aber keine echten Außenkanten des Dreiecks, sondern wir wissen, dass auch alles jenseits dieser Kante noch zum Dreieck gehört.
Eine Zeichnung:
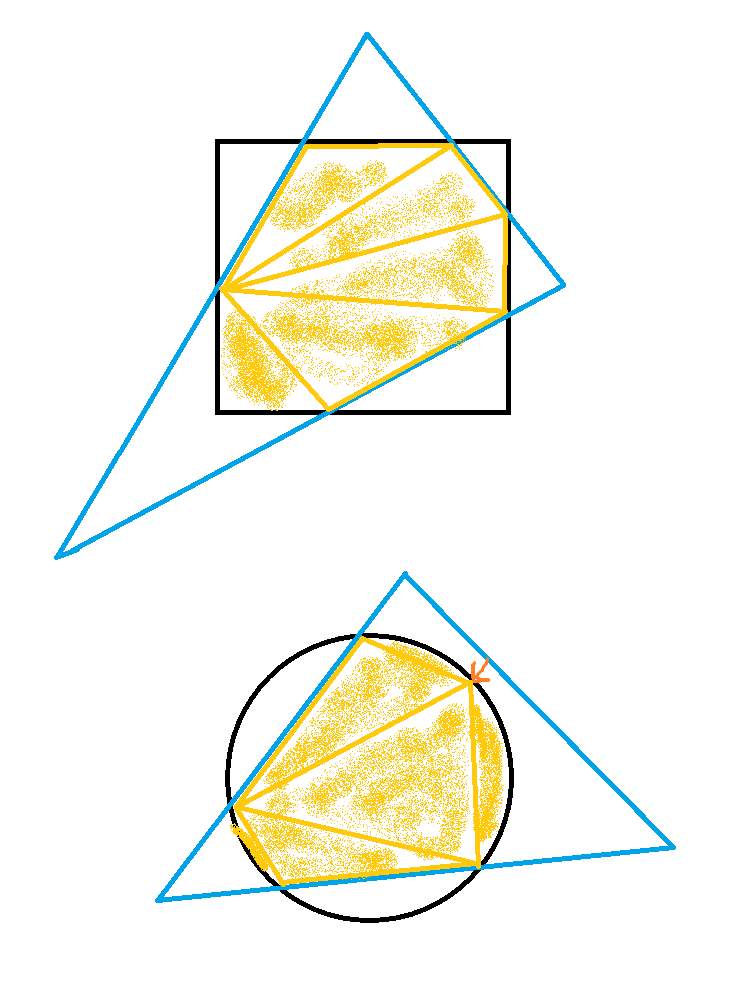
Exemplarisch für Quadrat und für Kreis, aber es würde so mit beliebigen konvexen Formen funktionieren. Man sieht hier, wo jede der drei Dreieckskanten in den Messbereich eintritt und wo sie austritt. Beim Kreis passiert eine Kante nur den Kreis, aber die quadratische Formel würde den nahesten Punkt plusminus eine nicht-reelle Wurzel auswerfen. Und da wir im Shader Ausnahmen und Fallunterscheidungen meiden, nehmen wir Ein- und Austritt der Kante halt an der Stelle des Kreises an.
Dann berechnen wir erstmal den Flächeninhalt aller Teil-Dreiecke, wie als wären alle Kanten Außenkanten des Dreiecks. Und dann kommt die Magie: wir addieren den Bereich hinter den Zwischenkanten obendrauf. Bei nem Quadrat / Rechteck ist das die Ecke hinter der Zwischenkante. Bei nem Kreis ist es ein Scheibchen von der Kreisfläche, und da der Kreis rotationssymmetrisch ist, ist uns völlig egal, wo der ist. Der Flächeninhalt dieses Kreisscheibchens berechnet sich nur aus seinem Abstand zum Kreisrand.
Das muss ich unbedingt mal ausprobieren. Damit könnte man Schatten für Sonne und allgemein kugelförmige Lichtquellen raycasten.
Ich habe inzwischen ne andere Idee gehabt, die für alle konvexen Messbereiche funktioniert: man rechnet den Flächeninhalt des zurechtgestutzten Dreiecks aus, wie als wäre nix. Und dann rechnet man für die Zwischen-Den-Kanten-Geraden die Außenflächen dazu. Die Strecken zwischen Kante-Eintritt-In-Messbereich und Kante-Austritt-Aus-Messbereich sind ja "echte" Kanten, die nehmen wir als echte Schrägen. Die Strecken zwischen Austritt-Vorkante-Aus-Messbereich und Eintritt-Nachfolgekante-In-Messbereich sind aber keine echten Außenkanten des Dreiecks, sondern wir wissen, dass auch alles jenseits dieser Kante noch zum Dreieck gehört.
Eine Zeichnung:
Exemplarisch für Quadrat und für Kreis, aber es würde so mit beliebigen konvexen Formen funktionieren. Man sieht hier, wo jede der drei Dreieckskanten in den Messbereich eintritt und wo sie austritt. Beim Kreis passiert eine Kante nur den Kreis, aber die quadratische Formel würde den nahesten Punkt plusminus eine nicht-reelle Wurzel auswerfen. Und da wir im Shader Ausnahmen und Fallunterscheidungen meiden, nehmen wir Ein- und Austritt der Kante halt an der Stelle des Kreises an.
Dann berechnen wir erstmal den Flächeninhalt aller Teil-Dreiecke, wie als wären alle Kanten Außenkanten des Dreiecks. Und dann kommt die Magie: wir addieren den Bereich hinter den Zwischenkanten obendrauf. Bei nem Quadrat / Rechteck ist das die Ecke hinter der Zwischenkante. Bei nem Kreis ist es ein Scheibchen von der Kreisfläche, und da der Kreis rotationssymmetrisch ist, ist uns völlig egal, wo der ist. Der Flächeninhalt dieses Kreisscheibchens berechnet sich nur aus seinem Abstand zum Kreisrand.
Das muss ich unbedingt mal ausprobieren. Damit könnte man Schatten für Sonne und allgemein kugelförmige Lichtquellen raycasten.
Früher mal Dreamworlds. Früher mal Open Asset Import Library. Heutzutage nur noch so rumwursteln.
- starcow
- Establishment
- Beiträge: 590
- Registriert: 23.04.2003, 17:42
- Echter Name: Mischa Schaub
- Wohnort: Zürich
- Kontaktdaten:
Re: Dreiecke rastern
Sehr cool! Ich habs jetzt zwar noch nicht geschafft, deine Idee in Gänze nachzuvollziehen, aber ich werde es morgen mit mehr Frische nochmals versuchen!
Ich habe auch nochmals intensiv über dem Problem gebrütet und habe nach langem probieren einen einfachen Ansatz gefunden, der keine Ausnahmen produzieren sollte, universell in jeder beliebigen Situation funktioniert und dessen Aufwand linear und zudem relativ gering ausfallen müsste.
Ich bin jeden Falls überzeugt, das dem so ist (und hoffe, dass ich es morgen auch noch bin) :-D.
Ich werde ihn morgen auf Papier bringen - heute reicht die Zeit leider nicht mehr.
Gruss starcow
Ich habe auch nochmals intensiv über dem Problem gebrütet und habe nach langem probieren einen einfachen Ansatz gefunden, der keine Ausnahmen produzieren sollte, universell in jeder beliebigen Situation funktioniert und dessen Aufwand linear und zudem relativ gering ausfallen müsste.
Ich bin jeden Falls überzeugt, das dem so ist (und hoffe, dass ich es morgen auch noch bin) :-D.
Ich werde ihn morgen auf Papier bringen - heute reicht die Zeit leider nicht mehr.
Gruss starcow
- starcow
- Establishment
- Beiträge: 590
- Registriert: 23.04.2003, 17:42
- Echter Name: Mischa Schaub
- Wohnort: Zürich
- Kontaktdaten:
Re: Dreiecke rastern
Das Problem mit dem konvexen Polygon ist ja, dass wir nicht davon ausgehen dürfen, dass die (orangen) Punkte bereits in einer richtigen (gültigen) Reihenfolge vorliegen. Liegen sie nämlich nicht in Reihe, führt das zu "falschen Diagonalen", wie du das Problem treffend benannt hast.
Der Trick ist nun, einfach dafür zu sorgen, dass unsere orangen Punkte immer "in Reihe" liegen.
Wenn man den Prozess vom Finden eines Schnittpunktes lapidar als "Frage" (Im Sinne von, Frage an den Computer) bezeichnet, muss man also blos die sich wiederholenden Fragen in der richtigen Reihenfolge stellen. Denn: Fragen muss ich ja ohnehin. In welcher Reihenfolge ich welche Fragen nun stelle, wird sich also in diesem Punkt auch nicht negativ auf die Laufzeit auswirken. Was für uns natürlich ein wünschbarer Nebeneffekt ist!
Auf die Lösung bin ich gekommen, weil ich mir folgende Szene konkret vorgestellt hatte. Und da ich glaube, dass es so auch anschaulicher und einfacher zu erklären ist, will ich bei diesem Bild bleiben.
Wir stellen uns vor, wir seien eine Ameise, die eine bestimmte Strecke ablaufen soll. Dabei bewegt sich die Ameise nur entlange der geometrischen Strecken, die uns das Quadrat und das Dreieck vorgeben. Auch bewegt sich die Ameise immer nur in der Richtung, in die der Strecken-Vektor zeigt (auf welchem sie sich gerade befindet). Diese Regel ist wichtig - mehr dazu später.
Nach folgendem Rezept, wird die Ameise nun das Polygon garantiert in einer gültigen Reihenfolge ablaufen:
1) Die Ameise schnappt sich einen beliebigen Punkt des Dreieck und prüft diesen darauf, ob sich dieser im Pixel-Quadrat befindet. Denn: Das Rezept funktioniert nur dann, wenn die Ameise garantiert ausserhalb des Pixel-Quadrates startet.
Sollte der gewählte Eckpunkt des Dreieckes tatsächlich im Quadrat liegen, nimmt sie einfach den nächsten und prüft diesen ebenfalls.
Falls sich dann auch beim 3 Eckpunkt herausstellen sollte, dass auch dieser im Quadrat liegt, ist die Aufgabe bereits beendet. Denn dann gilt:
Pixelhelligkeit = Dreiecksfläche.
Ich schreibe das so ausführlich, weil wir an dieser Stelle netterweise ohne Mehraufwand einen "Spezialfall" loswerden.
2) Hat die Ameise nun einen Eckpunkt des Dreiecks (Startpunkt) gefunden, der ausserhalb des Pixelquadrates liegt, läuft sie in Richtung des Strecken-Vektors los (zu den Vektoren später mehr).
3) Die Ameise läuft nun so lange weiter, bis sie auf eine Kreuzung (einen Strecken-Schnittpunkt) trifft. Sollte sie auf dem "zweiten" Eckpunkt des Dreicks angekommen - ohne auf eine Kreuzung getroffen zu sein, läuft sie einfach auf dem neuen Strecken-Vektor weiter. Natürlich auch wieder in der Richtung, in welche der Strecken-Vektor zeigt. Trifft sie aber auf eine Kreuzung, macht sie folgendes: *trommelwirbel* ... Sie markiert die Kreuzung mit einem orangen Punkt (ab hier beginnt das Punktesetzen) und... ... läuft einfach weiter! Dieser Schritt ist in einem gewissen Sinne speziell: Denn nur bei der ersten Kreuzung läuft sie einfach weiter geradeaus. Denn so befindet sie sich nun mit Sicherheit im Quadrat.
4) Die weitere Reise ist nun absolut simpel. Trifft die Ameise auf eine Kreuzung, markiert sie diese mit einem orangen Punkt und biegt ab, in Richtung "Vektoren-Laufrichtung". Um in der Bildsprache zu bleiben: Sie _muss_ abbiegen, darf aber _nicht_ in die Strasse mit der "verbotenen Fahrtrichtung".
Trifft sie auf keine Kreuzung, sonder auf eine Ecke (was anderes ist nicht möglich), markiert sie diese Ecke mit einem orangen Punkt und geht weiter.
5) Erreicht die Ameise eine Kreuzung, die bereits mit einem orangen Punkt markiert ist, ist die Reise beendet und das Polygon in einer "gültigen" Reihenfolge abgelaufen.
Wenn man nun die Ameise beobachtet, dann gehören die Pfade, auf denen sie läuft, entweder zum Dreieck oder zum Quadrat. Aber das ganze interessiert sie gar nicht - und sie weiss davon auch nichts. An einer Kreuzung welchselt sie einfach von Dreickspfad zu Pixelpfad oder umgekehrt.
Am Ende der Prozedur hättest du dann nicht nur die Eckpunkte eines konvexen Polygons, sondern auch eines, bei dem die Punkte garantiert in Reihe liegen - und damit die Flächenberechnung ein Klacks ist.
Einzig müsste man noch testen - nur Falls man keinen einzigen Schnittpunkt gefunden hat, ob einer der Quadratpunkte (es reicht ein einzelner, beliebiger), sich im Dreeick befindet.
Dann gälte: Pixelhelligkeit = 1.0
Das ist die Idee. Konkret für den Algorithmus würde das bedeuten, dass ich immer einen Strecken-Vektor als auserkorenen Kandidaten habe, mit welchem ich dann die anderen Vektoren auf Schnitt kontrolliere. Finde ich den Vektor mit dem räumlich nächsten (wichtig!) Schnittpunkt, wird dieser Vektor zu meinem neuen erkorenen "Haupt-Kadidaten" (mit diesem prüfe ich dann wieder die Anderen).
An dieser Stelle gibt es bestimmt weitere Optimierungsmöglichkeiten, die evident sein müssten. Denn wenn z.B. mein aktueller "Haupt-Kandidat" eine Line des Quadrates ist, muss man ja diesen Vektor nicht mit den weiteren Quadrat-Linien auf Schnitt testen.
Mir schwebt so eine Art verkettete Liste vor, die durchlaufen wird. Treffe ich auf eine Kreuzung, hänge ich etwas in dieser Liste um. Aber die Idee ist noch etwas halbgar und allenfalls zu umständlich. Alternativ könnte man mit geraden und ungeraden Listen-Einträgen (Liste mit Vektoren) arbeiten. Dabei besetzen die Dreicks-Vektoren die ungeraden und die Quadrat-Vektoren die geraden Listeneinträge. gerade auf gerade wird ebenso wenig getestet wie ungerade auf ungerade. Nur so als "Skizze"...
Eine wichtige Sache hatte ich blos gestreift, nicht aber konkret erklärt:
Das Rezept setzt voraus, dass der "Drehsinn" von Quadrat und Dreieck (also deren Vektoren) der selbe ist.
Ich glaube die Grafik zeigt dies recht anschaulich. Wenn ich die Punkte des Dreiecks nach ihren Einträgen im Buffer ablaufe (egal, bei welchem ich auch starte) ergibt sich daraus ja zwangsläufig ein räumlicher Drehsinn. Dieser muss der selbe sein, wie beim Quadrat!
Als Vorbereitung für die Szene muss man also einmal überprüfen, ob der Drehsinn des Dreiecks dem des Quadrates entspricht (letzteres ändert sich ja nicht). Sollte dies nicht der Fall sein, muss man die Vertices des Dreickes im Buffer "rückwärts" auslesen.
Eine weitere Sache habe ich jetzt noch nicht angesprochen, da ich mir auch gar nicht sicher bin, ob deine Idee nicht schneller ist. Aber Falls dir der Ansatz gefällt, müsste man sich noch überlegen, wie man mit der Siutation umgeht, wenn ein Dreickseckpunkt genau auf einer Quadratlinie zu liegen kommt. Ich sehe hier aber bereits Ansätze, wie sich das Problem relativ einfach lösen liese.
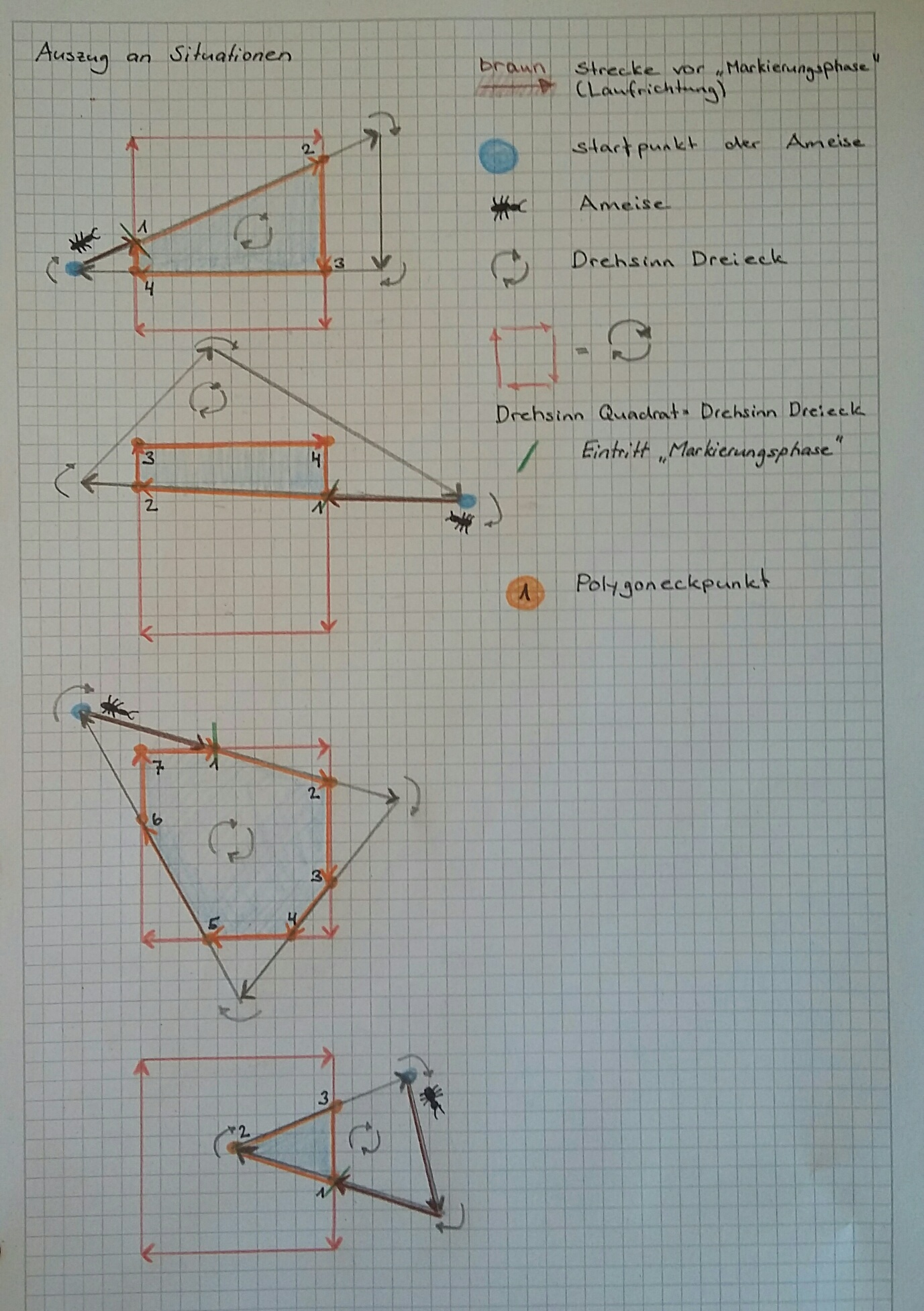
Der Trick ist nun, einfach dafür zu sorgen, dass unsere orangen Punkte immer "in Reihe" liegen.
Wenn man den Prozess vom Finden eines Schnittpunktes lapidar als "Frage" (Im Sinne von, Frage an den Computer) bezeichnet, muss man also blos die sich wiederholenden Fragen in der richtigen Reihenfolge stellen. Denn: Fragen muss ich ja ohnehin. In welcher Reihenfolge ich welche Fragen nun stelle, wird sich also in diesem Punkt auch nicht negativ auf die Laufzeit auswirken. Was für uns natürlich ein wünschbarer Nebeneffekt ist!
Auf die Lösung bin ich gekommen, weil ich mir folgende Szene konkret vorgestellt hatte. Und da ich glaube, dass es so auch anschaulicher und einfacher zu erklären ist, will ich bei diesem Bild bleiben.
Wir stellen uns vor, wir seien eine Ameise, die eine bestimmte Strecke ablaufen soll. Dabei bewegt sich die Ameise nur entlange der geometrischen Strecken, die uns das Quadrat und das Dreieck vorgeben. Auch bewegt sich die Ameise immer nur in der Richtung, in die der Strecken-Vektor zeigt (auf welchem sie sich gerade befindet). Diese Regel ist wichtig - mehr dazu später.
Nach folgendem Rezept, wird die Ameise nun das Polygon garantiert in einer gültigen Reihenfolge ablaufen:
1) Die Ameise schnappt sich einen beliebigen Punkt des Dreieck und prüft diesen darauf, ob sich dieser im Pixel-Quadrat befindet. Denn: Das Rezept funktioniert nur dann, wenn die Ameise garantiert ausserhalb des Pixel-Quadrates startet.
Sollte der gewählte Eckpunkt des Dreieckes tatsächlich im Quadrat liegen, nimmt sie einfach den nächsten und prüft diesen ebenfalls.
Falls sich dann auch beim 3 Eckpunkt herausstellen sollte, dass auch dieser im Quadrat liegt, ist die Aufgabe bereits beendet. Denn dann gilt:
Pixelhelligkeit = Dreiecksfläche.
Ich schreibe das so ausführlich, weil wir an dieser Stelle netterweise ohne Mehraufwand einen "Spezialfall" loswerden.
2) Hat die Ameise nun einen Eckpunkt des Dreiecks (Startpunkt) gefunden, der ausserhalb des Pixelquadrates liegt, läuft sie in Richtung des Strecken-Vektors los (zu den Vektoren später mehr).
3) Die Ameise läuft nun so lange weiter, bis sie auf eine Kreuzung (einen Strecken-Schnittpunkt) trifft. Sollte sie auf dem "zweiten" Eckpunkt des Dreicks angekommen - ohne auf eine Kreuzung getroffen zu sein, läuft sie einfach auf dem neuen Strecken-Vektor weiter. Natürlich auch wieder in der Richtung, in welche der Strecken-Vektor zeigt. Trifft sie aber auf eine Kreuzung, macht sie folgendes: *trommelwirbel* ... Sie markiert die Kreuzung mit einem orangen Punkt (ab hier beginnt das Punktesetzen) und... ... läuft einfach weiter! Dieser Schritt ist in einem gewissen Sinne speziell: Denn nur bei der ersten Kreuzung läuft sie einfach weiter geradeaus. Denn so befindet sie sich nun mit Sicherheit im Quadrat.
4) Die weitere Reise ist nun absolut simpel. Trifft die Ameise auf eine Kreuzung, markiert sie diese mit einem orangen Punkt und biegt ab, in Richtung "Vektoren-Laufrichtung". Um in der Bildsprache zu bleiben: Sie _muss_ abbiegen, darf aber _nicht_ in die Strasse mit der "verbotenen Fahrtrichtung".
Trifft sie auf keine Kreuzung, sonder auf eine Ecke (was anderes ist nicht möglich), markiert sie diese Ecke mit einem orangen Punkt und geht weiter.
5) Erreicht die Ameise eine Kreuzung, die bereits mit einem orangen Punkt markiert ist, ist die Reise beendet und das Polygon in einer "gültigen" Reihenfolge abgelaufen.
Wenn man nun die Ameise beobachtet, dann gehören die Pfade, auf denen sie läuft, entweder zum Dreieck oder zum Quadrat. Aber das ganze interessiert sie gar nicht - und sie weiss davon auch nichts. An einer Kreuzung welchselt sie einfach von Dreickspfad zu Pixelpfad oder umgekehrt.
Am Ende der Prozedur hättest du dann nicht nur die Eckpunkte eines konvexen Polygons, sondern auch eines, bei dem die Punkte garantiert in Reihe liegen - und damit die Flächenberechnung ein Klacks ist.
Einzig müsste man noch testen - nur Falls man keinen einzigen Schnittpunkt gefunden hat, ob einer der Quadratpunkte (es reicht ein einzelner, beliebiger), sich im Dreeick befindet.
Dann gälte: Pixelhelligkeit = 1.0
Das ist die Idee. Konkret für den Algorithmus würde das bedeuten, dass ich immer einen Strecken-Vektor als auserkorenen Kandidaten habe, mit welchem ich dann die anderen Vektoren auf Schnitt kontrolliere. Finde ich den Vektor mit dem räumlich nächsten (wichtig!) Schnittpunkt, wird dieser Vektor zu meinem neuen erkorenen "Haupt-Kadidaten" (mit diesem prüfe ich dann wieder die Anderen).
An dieser Stelle gibt es bestimmt weitere Optimierungsmöglichkeiten, die evident sein müssten. Denn wenn z.B. mein aktueller "Haupt-Kandidat" eine Line des Quadrates ist, muss man ja diesen Vektor nicht mit den weiteren Quadrat-Linien auf Schnitt testen.
Mir schwebt so eine Art verkettete Liste vor, die durchlaufen wird. Treffe ich auf eine Kreuzung, hänge ich etwas in dieser Liste um. Aber die Idee ist noch etwas halbgar und allenfalls zu umständlich. Alternativ könnte man mit geraden und ungeraden Listen-Einträgen (Liste mit Vektoren) arbeiten. Dabei besetzen die Dreicks-Vektoren die ungeraden und die Quadrat-Vektoren die geraden Listeneinträge. gerade auf gerade wird ebenso wenig getestet wie ungerade auf ungerade. Nur so als "Skizze"...
Eine wichtige Sache hatte ich blos gestreift, nicht aber konkret erklärt:
Das Rezept setzt voraus, dass der "Drehsinn" von Quadrat und Dreieck (also deren Vektoren) der selbe ist.
Ich glaube die Grafik zeigt dies recht anschaulich. Wenn ich die Punkte des Dreiecks nach ihren Einträgen im Buffer ablaufe (egal, bei welchem ich auch starte) ergibt sich daraus ja zwangsläufig ein räumlicher Drehsinn. Dieser muss der selbe sein, wie beim Quadrat!
Als Vorbereitung für die Szene muss man also einmal überprüfen, ob der Drehsinn des Dreiecks dem des Quadrates entspricht (letzteres ändert sich ja nicht). Sollte dies nicht der Fall sein, muss man die Vertices des Dreickes im Buffer "rückwärts" auslesen.
Eine weitere Sache habe ich jetzt noch nicht angesprochen, da ich mir auch gar nicht sicher bin, ob deine Idee nicht schneller ist. Aber Falls dir der Ansatz gefällt, müsste man sich noch überlegen, wie man mit der Siutation umgeht, wenn ein Dreickseckpunkt genau auf einer Quadratlinie zu liegen kommt. Ich sehe hier aber bereits Ansätze, wie sich das Problem relativ einfach lösen liese.
- Schrompf
- Moderator
- Beiträge: 5330
- Registriert: 25.02.2009, 23:44
- Benutzertext: Lernt nur selten dazu
- Echter Name: Thomas
- Wohnort: Dresden
- Kontaktdaten:
Re: Dreiecke rastern
Wenn ich das richtig verstanden habe, wird das funktionieren. Danke für die ausführliche Erklärung und die schicken Skizzen. Es ist nur leider eine sehr un-gpu-ige Lösung. Jede Menge bedingte Verzweigungen. Heutige GPUs würden das mitmachen, würden dabei aber ziemlich viel leer laufen.
Früher mal Dreamworlds. Früher mal Open Asset Import Library. Heutzutage nur noch so rumwursteln.
- starcow
- Establishment
- Beiträge: 590
- Registriert: 23.04.2003, 17:42
- Echter Name: Mischa Schaub
- Wohnort: Zürich
- Kontaktdaten:
Re: Dreiecke rastern
Ok, schade. Leider verstehe ich deinen Ansatz nicht wirklich. Versuche es aber später nochmals... Wenn ich dich recht verstehe, dann ist quasi "if" tabu. Was machst du denn, wenn ein Dreieckspunkt im Quadrat zu liegen kommt? Ich komm auch nicht drauf, wie du ohne if feststellen kannst, ob eine Gerade eine andere schneidet und welche allenfalls die nähere ist.
Edit:
Alleine wenn du den Schnittpunkt zweier Strecken finden willst, brauchst du ja std::max(std::min(1.0, scale), 0.0) oder alternativ clamp(), um festzustellen, ob der Schnittpunkt der Geraden noch auf dem Streckenbereich liegt. Und dann musst du ja zwingend den "scale" mit dem tiefsten Wert finden. Alleine für clamp() muss ja die GPU vergleichen und dem Entweder-Oder-Prinzip nach eine Operation ausführen.
Stehst du dann rechnerisch nicht genau am selben Punkt wie ich?
Edit:
Alleine wenn du den Schnittpunkt zweier Strecken finden willst, brauchst du ja std::max(std::min(1.0, scale), 0.0) oder alternativ clamp(), um festzustellen, ob der Schnittpunkt der Geraden noch auf dem Streckenbereich liegt. Und dann musst du ja zwingend den "scale" mit dem tiefsten Wert finden. Alleine für clamp() muss ja die GPU vergleichen und dem Entweder-Oder-Prinzip nach eine Operation ausführen.
Stehst du dann rechnerisch nicht genau am selben Punkt wie ich?
Re: Dreiecke rastern
@starcow
Also du kannst schon Fallunterscheidungen machen, aber du musst bedenken, dass im schlechtesten Fall eben alles berechnet wird. Stell dir vor, du rechnest ALLE Fallunterscheidungen aus und wählst am Ende das Ergebnis, welches du in dem Fall brauchst. Bedeutet auch, dass man mit einem if nicht einfach optimieren kann indem bestimmter Code übersprungen wird.
(Ist natürlich nicht ganz richtig, denn es ist dann doch um einiges komplizierter. Grob zusammengefasst würde ich sagen, wenn ganze Bildabschnitte den selben Shaderzweig wählen KANN ein if optimierend wirken. Aber das hängt an vielen Faktoren.)
Also du kannst schon Fallunterscheidungen machen, aber du musst bedenken, dass im schlechtesten Fall eben alles berechnet wird. Stell dir vor, du rechnest ALLE Fallunterscheidungen aus und wählst am Ende das Ergebnis, welches du in dem Fall brauchst. Bedeutet auch, dass man mit einem if nicht einfach optimieren kann indem bestimmter Code übersprungen wird.
(Ist natürlich nicht ganz richtig, denn es ist dann doch um einiges komplizierter. Grob zusammengefasst würde ich sagen, wenn ganze Bildabschnitte den selben Shaderzweig wählen KANN ein if optimierend wirken. Aber das hängt an vielen Faktoren.)
- starcow
- Establishment
- Beiträge: 590
- Registriert: 23.04.2003, 17:42
- Echter Name: Mischa Schaub
- Wohnort: Zürich
- Kontaktdaten:
Re: Dreiecke rastern
Ich hab jetzt mal versucht, bisschen konkreten Code dazu zu schreiben.
Ganz hab ichs jetzt nicht fertig gemacht, weil die Vermutung von Schrompf vermutlich stimmen dürfte.
Die spezielle Situation beim "Eintreten" ist noch nicht berücksichtigt. Aber von der Logik her, ist es ungefähr das:
Ein Versuch wars wert! ^^
Gruss starcow
Ganz hab ichs jetzt nicht fertig gemacht, weil die Vermutung von Schrompf vermutlich stimmen dürfte.
Die spezielle Situation beim "Eintreten" ist noch nicht berücksichtigt. Aber von der Logik her, ist es ungefähr das:
Code: Alles auswählen
struct STR_Vector {
double ox, oy;
double x, y;
STR_Vector* Next;
};
std::vector<STR_Vector> polygon;
STR_Vector* StartTriangle;
STR_Vector* StartSquare;
STR_Vector* Candidate;
STR_Vector* Compare;
STR_Vector* NextCandidate;
STR_Vector* NextCompare;
STR_Vector* StartCompare;
double scale = 1.0;
double intersect = 1.0;
// StartTriangle holen
// StartSquare holen
Candidate = StartTriangle;
Compare = StartSquare;
do {
NextCandidate = Candidate->Next;
NextCompare = Compare;
StartCompare = Compare;
scale = 1.0;
do {
intersect = Compare.intersect(Candidate); // Vektoren schneiden und einen Skalierungsfaktor für Compare zurückgeben
if (intersect > 0.0 && intersect < scale) {
scale = intersect;
NextCandidate = Compare;
NextCompare = Candidate;
}
Compare = Compare->Next;
} while (Compare != StartCompare);
Candidate = NextCandidate;
Compare = NextCompare;
polygon.push_back((*Candidate) * scale);
} while (Compare != StartTriangle);
}
Gruss starcow
Re: Dreiecke rastern
Oha... also noch schlimmer als If im Shader sind natürlich Schleifen, wenn diese verschieden terminieren.
Das einzige, was mir einfällt, was noch schlimmer ist, sind verschachtelte Schleifen :D
Okay, vielleicht ist das bei neueren Shadern nicht mehr soooo schlimm... aber früher war es das auf jeden Fall.
Vielleicht schaffst du es ja, das Ganze GPU freindlich umzubauen. Dabei kannst du ruhig etwas krude Wege einschlagen... Gleitkommaberechnungen sind ja fast umsonst.
Du könntest z.B. für Zuweisungen bei Fallunterscheidungen eine Interpolation machen.
In etwa so:
condition = step(0, intersect) * step(intersect, scale); // weiß jetzt nicht genau, wie rum das alles gehört. Will nur das vorgehen verdeutlichen
scale = mix(scale, intersect, condition);
NextCandidate = mix(NextCandidate, Compare, condition);
NextCompare = mix(NextCompare, Candidate, condition);
Also es wird immer der alte Wert weiter geführt, außer die Bedingung erfüllt sich. Würde man auf CPU so niemals machen. Bei der GPU muss man dann messen, welche Varianten am schnellsten sind. Aber das hängt dann auch nochmal von Grafikkarte und Treiber ab soweit ich weiß.
Bei den oben genannten Konstrukten muss man noch beachten, dass man am besten immer mit 4D Vektoren arbeitet, damit bekommt man dann das vierfache an Geschwindigkeit geschenkt. Allerdings würde sich bei dem erwähnten beispiel eher anbieten, wenn man die 3 variablen in einen 3D Vektor packt... dann hätte man da für die Zuweisung nur ein mix. Bietet sich bei deinem Algo wahrscheinlich eher an als 4 Bedingungen parallel zu prüfen. Weil, wenn ich das richtig verstanden habe, die Ergebnisse ja aufeinander aufbauen wegen der Reihenfolge.
Noch ein anregendes Bild zur Ideenfindung... oder vielleicht auch nicht... scheint ja bei den Mäusemampfern nicht so exakt zu funktionieren :D

Das einzige, was mir einfällt, was noch schlimmer ist, sind verschachtelte Schleifen :D
Okay, vielleicht ist das bei neueren Shadern nicht mehr soooo schlimm... aber früher war es das auf jeden Fall.
Vielleicht schaffst du es ja, das Ganze GPU freindlich umzubauen. Dabei kannst du ruhig etwas krude Wege einschlagen... Gleitkommaberechnungen sind ja fast umsonst.
Du könntest z.B. für Zuweisungen bei Fallunterscheidungen eine Interpolation machen.
In etwa so:
condition = step(0, intersect) * step(intersect, scale); // weiß jetzt nicht genau, wie rum das alles gehört. Will nur das vorgehen verdeutlichen
scale = mix(scale, intersect, condition);
NextCandidate = mix(NextCandidate, Compare, condition);
NextCompare = mix(NextCompare, Candidate, condition);
Also es wird immer der alte Wert weiter geführt, außer die Bedingung erfüllt sich. Würde man auf CPU so niemals machen. Bei der GPU muss man dann messen, welche Varianten am schnellsten sind. Aber das hängt dann auch nochmal von Grafikkarte und Treiber ab soweit ich weiß.
Bei den oben genannten Konstrukten muss man noch beachten, dass man am besten immer mit 4D Vektoren arbeitet, damit bekommt man dann das vierfache an Geschwindigkeit geschenkt. Allerdings würde sich bei dem erwähnten beispiel eher anbieten, wenn man die 3 variablen in einen 3D Vektor packt... dann hätte man da für die Zuweisung nur ein mix. Bietet sich bei deinem Algo wahrscheinlich eher an als 4 Bedingungen parallel zu prüfen. Weil, wenn ich das richtig verstanden habe, die Ergebnisse ja aufeinander aufbauen wegen der Reihenfolge.
Noch ein anregendes Bild zur Ideenfindung... oder vielleicht auch nicht... scheint ja bei den Mäusemampfern nicht so exakt zu funktionieren :D

- Schrompf
- Moderator
- Beiträge: 5330
- Registriert: 25.02.2009, 23:44
- Benutzertext: Lernt nur selten dazu
- Echter Name: Thomas
- Wohnort: Dresden
- Kontaktdaten:
Re: Dreiecke rastern
Branching auf GPUs ist immer noch "teuer". Du musst Dir ne GPU wie ein CPU-Kern vorstellen, der ~64 mal verschiedene Zahlen verrechnet. Es gibt quasi einen Scheduler, der bestimmt, was als Anweisung gemacht wird, aber 64 verschiedene Parameter für diese Anweisung. Ein if( cond ) wertet die Bedingung aus, und wenn auch nur ein einziger von den 64 Threads ein anderes Ergebnis bringt, marschiert die gesamte Kompanie durch beide Wege. Eine Schleife läuft so lange, bis auch der letzte der 64 Threads zufrieden ist, und schlimmstenfalls marschieren 63 Threads leer mit (und äußern dabei hässliche Worte über die Mutter des Threads).
Die neueste NVidia-Generation - Volta oder so? Hab den Überblick verloren - hat übrigens neben den normalen GPU-Pipelines noch sogenannte Tensor-Cores, und soweit ich weiß, haben die tatsächlich einen Scheduler pro Thread, wie ne normale CPU. Aber die gibt's nur in Server-Grafikkarten für High Performance Computing, und NVidia bezahlt das sehr teuer mit Chipfläche. Ich hab irgendwas von 20 Milliarden Transistoren vs. 7 Milliarden Transistoren im Hinterkopf. Aber wie immer alle Angaben ohne Gewähr.
Die neueste NVidia-Generation - Volta oder so? Hab den Überblick verloren - hat übrigens neben den normalen GPU-Pipelines noch sogenannte Tensor-Cores, und soweit ich weiß, haben die tatsächlich einen Scheduler pro Thread, wie ne normale CPU. Aber die gibt's nur in Server-Grafikkarten für High Performance Computing, und NVidia bezahlt das sehr teuer mit Chipfläche. Ich hab irgendwas von 20 Milliarden Transistoren vs. 7 Milliarden Transistoren im Hinterkopf. Aber wie immer alle Angaben ohne Gewähr.
Früher mal Dreamworlds. Früher mal Open Asset Import Library. Heutzutage nur noch so rumwursteln.
- starcow
- Establishment
- Beiträge: 590
- Registriert: 23.04.2003, 17:42
- Echter Name: Mischa Schaub
- Wohnort: Zürich
- Kontaktdaten:
Re: Dreiecke rastern
Ich hätte vielleicht noch einen alternativen Ansatz.
Aber bevor ich jetzt versuche konkret einen Algorithmus dazu auszuarbeiten, vielleicht eine Einschätzung von euch, ob sowas genug schnell sein könnte.
Die Idee ist nämlich relativ einfach und funktioniert, soweit ich es abschätzen kann, auch ohne Ausnahmen.
Der Ansatz ist, dass die Polygonfläche (ganz egal, wie das konkrete Resultat auch ausschauen mag), immer durch drei Schnitte zustande kommt.
Die Fläche bleibt auch immer konvex. Daraus folgt, dass die einzelnen Eckpunkte, die ich mit den jeweiligen Schnitten abtrenne, immer zusammenhängend sein müssen. Ein weiteres Gesetzt ist, dass egal wie viele Eckpunkte ich abtrenne, nur zwei neue dazukommen - sofern ich mindestens ein Eckpunkt abtrenne.
Insofern ist es nicht weiter schwierig, die neuen Punkte in der richtigen Reihenfolge in die Struktur einzufügen, um das Problem mit den falschen Diagonalen zu lösen.
Topologisch bleibt die Szene nämlich immer ganz einfach.
Bei einem Schnitt braucht man blos beachten, auf welcher Seite des Schnittes der letzte Dreieckspunk liegt (ich meine damit das Dreieck, auf dessen Grundlage man die Schnitte ansetzt - also das zu rendernde Dreieck). Ob ein Eckpunkt "hüben oder drüben" liegt, lässt sich mit dem Skalarprodukt sehr schnell und einfach entscheiden.
Folgende Skizze, soll es verdeutlichen:
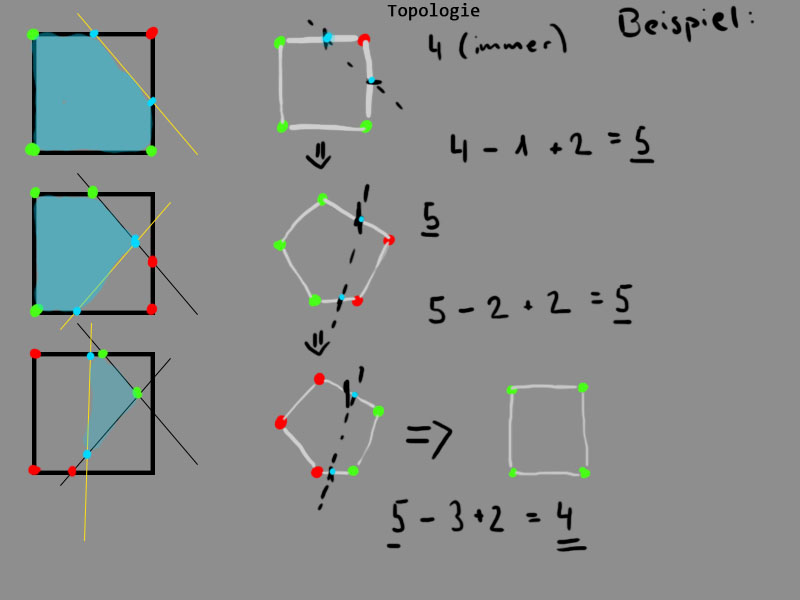
Vielleicht lässt sich ja diese Idee so umsetzen, dass der Rechnungsaufwand klein ausfällt?
Gruss starcow
Edit:
Kann ich denn eigentlich nicht einfach nur die Pixel prüfen, die von den drei Kanten auch tatsächlich geschnitten werden? Das müsste sich ja eigentlich gut vorselektionieren lassen.
Oder vielleicht eine Bounding-Box um das Dreieck legen und dann nur die Pixel prüfen, die innerhalb dieses Rechteckes liegen.
Es ist zudem ohnehin so, dass mit dieser Methode nur in den seltensten Fällen in die Struktur eingegriffen werden muss. Somit müssten sich die meisten Fällen sehr schnell entscheiden lassen. Denn oftmals wird einfach alles oder gar nichts "abgeschnitten".
Edit 2:
Vielleicht lässt sich das ganze ja noch parallelisieren? Also dass man die verschiedenen Dreiecke auf verschiedene Threads verteilt?
Aber bevor ich jetzt versuche konkret einen Algorithmus dazu auszuarbeiten, vielleicht eine Einschätzung von euch, ob sowas genug schnell sein könnte.
Die Idee ist nämlich relativ einfach und funktioniert, soweit ich es abschätzen kann, auch ohne Ausnahmen.
Der Ansatz ist, dass die Polygonfläche (ganz egal, wie das konkrete Resultat auch ausschauen mag), immer durch drei Schnitte zustande kommt.
Die Fläche bleibt auch immer konvex. Daraus folgt, dass die einzelnen Eckpunkte, die ich mit den jeweiligen Schnitten abtrenne, immer zusammenhängend sein müssen. Ein weiteres Gesetzt ist, dass egal wie viele Eckpunkte ich abtrenne, nur zwei neue dazukommen - sofern ich mindestens ein Eckpunkt abtrenne.
Insofern ist es nicht weiter schwierig, die neuen Punkte in der richtigen Reihenfolge in die Struktur einzufügen, um das Problem mit den falschen Diagonalen zu lösen.
Topologisch bleibt die Szene nämlich immer ganz einfach.
Bei einem Schnitt braucht man blos beachten, auf welcher Seite des Schnittes der letzte Dreieckspunk liegt (ich meine damit das Dreieck, auf dessen Grundlage man die Schnitte ansetzt - also das zu rendernde Dreieck). Ob ein Eckpunkt "hüben oder drüben" liegt, lässt sich mit dem Skalarprodukt sehr schnell und einfach entscheiden.
Folgende Skizze, soll es verdeutlichen:
Vielleicht lässt sich ja diese Idee so umsetzen, dass der Rechnungsaufwand klein ausfällt?
Gruss starcow
Edit:
Kann ich denn eigentlich nicht einfach nur die Pixel prüfen, die von den drei Kanten auch tatsächlich geschnitten werden? Das müsste sich ja eigentlich gut vorselektionieren lassen.
Oder vielleicht eine Bounding-Box um das Dreieck legen und dann nur die Pixel prüfen, die innerhalb dieses Rechteckes liegen.
Es ist zudem ohnehin so, dass mit dieser Methode nur in den seltensten Fällen in die Struktur eingegriffen werden muss. Somit müssten sich die meisten Fällen sehr schnell entscheiden lassen. Denn oftmals wird einfach alles oder gar nichts "abgeschnitten".
Edit 2:
Vielleicht lässt sich das ganze ja noch parallelisieren? Also dass man die verschiedenen Dreiecke auf verschiedene Threads verteilt?
- starcow
- Establishment
- Beiträge: 590
- Registriert: 23.04.2003, 17:42
- Echter Name: Mischa Schaub
- Wohnort: Zürich
- Kontaktdaten:
Re: Dreiecke rastern
Ist das Projekt auf Eis gelegt oder taugt mein Ansatz nichts? Oder vielleicht beides? (-:
LG, starcow
LG, starcow
- Schrompf
- Moderator
- Beiträge: 5330
- Registriert: 25.02.2009, 23:44
- Benutzertext: Lernt nur selten dazu
- Echter Name: Thomas
- Wohnort: Dresden
- Kontaktdaten:
Re: Dreiecke rastern
Ich hab mir das damals durchgelesen, aber das ist nicht konkret genug, um was dazu zu sagen. Das Abschnippeln von Ecken finde ich sexy, aber im Shader kann man eigentlich nicht dynamisch in Listen oder Arrays rumstapeln. Und daher ist ne Lösung, die dynamisch einen Punkt hinzufügt, nicht wirklich machbar. Aber wenn Du was weißt, das ich nicht kenne, mach doch ne kleine Demo im ShaderToy. Ich bin interessiert.
Parallelisieren fängt man nicht auf diesem Level an. Das Starten eines Stücks Code dauert selbst auf der CPU einige Mikrosekunden, bevor es überhaupt losläuft. Bis dahin bist Du mit dutzenden Dreiecken durch. Auf der GPU reden wir nach HW-Architektur, Scheduler und verwendeter Tech eher von Millisekunden.
Parallelisieren fängt man nicht auf diesem Level an. Das Starten eines Stücks Code dauert selbst auf der CPU einige Mikrosekunden, bevor es überhaupt losläuft. Bis dahin bist Du mit dutzenden Dreiecken durch. Auf der GPU reden wir nach HW-Architektur, Scheduler und verwendeter Tech eher von Millisekunden.
Früher mal Dreamworlds. Früher mal Open Asset Import Library. Heutzutage nur noch so rumwursteln.
- starcow
- Establishment
- Beiträge: 590
- Registriert: 23.04.2003, 17:42
- Echter Name: Mischa Schaub
- Wohnort: Zürich
- Kontaktdaten:
Re: Dreiecke rastern
Ok, dann wirds wohl tatsächlich schwierig, leider :-/. Ich hatte noch überlegt, ob man vielleicht eine Baumstrucktur darauf anwenden könnte - mit dem Gedanken, ein statisches Array zu verwenden, das einfach Felder erstmal "unbenutzt" lässt, solange die entsprechende Ecke noch nicht abgeschnitten wurde. Aber ich vermute, das wird zu kompliziert.
LG, starcow
LG, starcow
- Schrompf
- Moderator
- Beiträge: 5330
- Registriert: 25.02.2009, 23:44
- Benutzertext: Lernt nur selten dazu
- Echter Name: Thomas
- Wohnort: Dresden
- Kontaktdaten:
Re: Dreiecke rastern
Naja, vielleicht nicht ganz. Mir fällt gerade auf, dass Du damit quasi TimSweeney's Idee des BSP-Trees skizziert hast: eine Gerade durch die Grundfläche ziehen, die das Gebiet in zwei Hälften teilt - "gehört dazu" und "gehört nicht dazu". Man darf den Tree halt nicht direkt so bauen, sondern müsste ein Array von Einträgen aufbauen, die jeweils per Index auf ihre Teilstücke verweisen. Das geht zumindest im Compute Shader, wenn auch sicher nicht im Fragment Shader.
Für diesen limitierten Anwendungsfall "Ein Dreieck gegen Grundfläche" könnte man aber alle Sonderfälle einfach fest zugunsten des WorstCase auflösen. Also immer zwei Punkte einsetzen, wenn der Schnitt 0 bis 2 Punkte ergeben könnte. Und die Punkte müssten dann halt so landen, dass sie im schlimmsten Fall ne Null-Fläche ergeben, dann kommst Du komplett ohne Fallunterscheidungen raus.
Und ich glaube, ohne es nachgerechnet zu haben, dass Du dann quasi das Gleiche machst wie ich in meiner letztenLösung.
Für diesen limitierten Anwendungsfall "Ein Dreieck gegen Grundfläche" könnte man aber alle Sonderfälle einfach fest zugunsten des WorstCase auflösen. Also immer zwei Punkte einsetzen, wenn der Schnitt 0 bis 2 Punkte ergeben könnte. Und die Punkte müssten dann halt so landen, dass sie im schlimmsten Fall ne Null-Fläche ergeben, dann kommst Du komplett ohne Fallunterscheidungen raus.
Und ich glaube, ohne es nachgerechnet zu haben, dass Du dann quasi das Gleiche machst wie ich in meiner letztenLösung.
Früher mal Dreamworlds. Früher mal Open Asset Import Library. Heutzutage nur noch so rumwursteln.